webové stránky vědy a techniky

výpočty

9. 4. 2008

fyzikální rovnice jsou určené k počítání čísel pomocí rovnic spojené s počítáním rovnicovitých výpočtů fyzikálních rovnic.

Uvažujme dvě funkce $f (x), g (x)$ , které jsou definovány na nějaké množině $D$ , pak nalezení všech 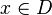$x \in D$ , která splňují rovnost

f (x) = g (x)

se nazývá rovnicí o jedné neznámé $x$ . Funkce $f (x)$ se nazývá levá strana rovnice a $g (x)$ se nazývá pravá strana rovnice.

Podrobnější informace naleznete v článku Kořen (matematika).

Každé číslo 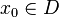$x_0 \in D$ , které vyhovuje vztahu $f (x 0) = g (x 0)$ , se nazývá kořen rovnice. Množinu všech kořenů dané rovnice označujeme jako řešení rovnice. Má-li rovnice alespoň jeden kořen v $D$ , nazývá se řešitelná v $D$ , pokud žádný kořen v $D$ nemá, říkáme, že rovnice je v $D$ neřešitelná. Pokud je rovnice $f (x) = g (x)$ splněna pro všechna 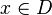$x \in D$ , jde o identitu, což značíme

$f(x) \equiv g(x)$

[editovat] Triviální řešení

Řešení, které je identicky rovno nule, se označuje jako triviální. Pokud řešení rovnice není identicky rovno nule, hovoří se o netriviálním řešení.

V mnoha případech přímo součástí zadání problému požadavek na nalezení pouze netriviálního řešení.

Např. triviálním řešením diferenciální rovnice

$y^\prime = y$

y = 0

což je funkce identicky rovna nule. Netriviální řešení má tvar

y = e x

což je exponenciální funkce.

Jiným příkladem je tzv. Velká Fermatova věta, která hledá netriviální řešení rovnice $a n + b n = c n$ pro $n > 2$ . Triviálním řešením by v tomto případě bylo $a = b = c = 0$ , což platí pro libovolné $n$ . Podobně je triviálním řešením $a = 1, b = 0, c = 1$ . Takováto řešení jsou však obvykle nezajímavá.

Jsou-li na dané množině definovány dvě rovnice $f 1 (x) = g 1 (x), f 2 (x) = g 2 (x)$ , pak je-li každý kořen první rovnice současně kořenem rovnice druhé a naopak, říkáme, že obě rovnice jsou ekvivalentní.

Rovnici lze tzv. ekvivalentními úpravami převést na ekvivalentní rovnici. Mezi nejčastěji používané ekvivalentní úpravy patří:

přičtení (nebo odečtení) stejného čísla k oběma stranám rovnice, tzn. $f (x) + a = g (x) + a$ je ekvivalentní rovnicí s rovnicí $f (x) = g (x)$
vynásobení obou stran rovnice stejným nenulovým číslem, tzn. $a f (x) = a g (x)$ je ekvivalentní rovnicí s rovnicí $f (x) = g (x)$

Rovnici $f (x) = g (x)$ je možné pomocí ekvivalentních úprav převést na (ekvivalentní) tvar

F (x) = f (x) - g (x) = 0

Při řešení rovnice lze použít také jiné úpravy, např. logaritmování nebo umocnění obou stran rovnice apod. Tyto úpravy však nemusí být ekvivalentní a při jejich použití je vždy nutno provést zkoušku.

[editovat] Zkouška

Po nalezení řešení rovnice provádíme zkoušku, neboť v mnoha případech nejsme schopni ověřit, zda použité úpravy byly opravdu ekvivalentní. Zkouška spočívá v dosazení získaných kořenů do původní rovnice. Pokud některý kořen nesplňuje zkoušku, nebyly pravděpodobně všechny provedené úpravy ekvivalentní, a nejedná se tedy o kořen původní rovnice.

[editovat] Rovnice o více neznámých

Rovnice o $n$ neznámých má tvar

F (x 1, x 2,..., x n) = 0

Při jejím řešení postupujeme obdobně jako při řešení rovnice o jedné neznámě $F (x) = 0$ , přičemž řešením rovnice o $n$ neznámých jsou n-tice $(x 1, x 2,..., x n)$ .

[editovat] Algebraické a nealgebraické rovnice

Rovnice lze rozdělit na algebraické rovnice (též označované jako polynomiální rovnice) a nealgebraické rovnice (též transcendentní rovnice).

Jako algebraickou rovnici $n$ -tého stupně o jedné neznámé označujeme rovnici ve tvaru

a n x n + a n - 1 x n - 1 + ... + a 1 x + a 0 = 0

kde levou stranu rovnice tvoří polynom $n$ -tého stupně s 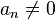$a_n \neq 0$ , přičemž se předpokládá, že $n \geq 1$ . Pokud rovnici nelze vyjádřit ve tvaru algebraické rovnice, pak hovoříme o rovnici nealgebraické.

Rovnice až do 4. stupně jsou obecně vždy řešitelné analyticky, v algebře se dokazuje, že obecný vzorec řešící jakoukoli rovnici 5. a vyšších stupňů neexistuje a řešení je nutné hledat numericky.

Mezi nejjednodušší algebraické rovnice patří lineární rovnice $(n = 1)$ , kvadratická rovnice $(n = 2)$ , kubická rovnice $(n = 3)$ a kvartická rovnice $(n = 4)$ . Také pro některé zvláštní případy polynomů dostáváme jednoduché rovnice, jde např. o binomické, trinomické nebo reciproké rovnice.

Při práci s algebraickými rovnicemi má velký význam tzv. základní věta algebry. Podle této věty má každý polynom s komplexními koeficienty stupně $n \geq 1$ alespoň jeden komplexní kořen. Každá algebraická rovnice má tedy řešení v oboru komplexníxh čísel. Řešení algebraických rovnic usnadňuje znalost některých vlastností polynomů.

Mezi nejjednodušší případy nealgebraických rovnic patří např. exponenciální rovnice, logaritmická rovnice nebo goniometrická rovnice.

[editovat] Homogenní rovnice

Algebraickou rovnici o několika neznámých označujeme jako homogenní, pokud mají všechny její členy stejný stupeň. Např. $3 x 2 y + 3 x 3 + 2 y 3 - 5 x y 2 = 0$ je homogenní rovnice třetího stupně.

Homogenní rovnici lze vyjádřit ve tvaru $f (x) = 0$ , kde $f (x)$ je homogenní funkce.

a tohle jsou rovnice

Komentáře

Přehled komentářů

Zatím nebyl vložen žádný komentář

Menu